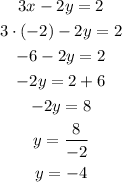Question

Solve for x and y3x - 2y = 25x - 5y = 10

Answer 1

• x = -2

,

• y = -4

Step-by-step explanation

The elimination method consists in subtracting one equation from the other in order to eliminate one of the variables, obtaining one equation with one variable. In some cases we have to multiply or divide the whole equation by a factor.

In this case, note that if we multiply the second equation by 2 and the first equation by 5, in both we'll have -10y:

`\begin{gathered} 5\cdot(3x-2y=2) \\ 15x-10y=10 \end{gathered}`
`\begin{gathered} 2\cdot(5x-5y=10) \\ 10x-10y=20 \end{gathered}`

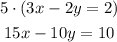
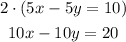
Now subtracting the first equation from the second:

`\begin{gathered} 10x-10y=20 \\ - \\ 15x-10y=10 \\ \text{ -----------------------------} \\ (10x-15x)+(-10y-10y)=20-10 \\ -5x+0=10 \\ -5x=10 \end{gathered}`

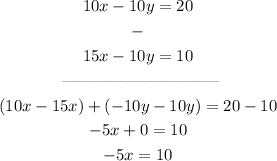
Solving for x:

`\begin{gathered} -5x=10 \\ x=(10)/(-5) \\ x=-2 \end{gathered}`

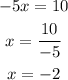
Now, to find y, we just have to replace x = -2 into any of the equations and solve for y. In this case, I'll replace it in the first equation:

`\begin{gathered} 3x-2y=2 \\ 3\cdot(-2)-2y=2 \\ -6-2y=2 \\ -2y=2+6 \\ -2y=8 \\ y=(8)/(-2) \\ y=-4 \end{gathered}`