Question

Find sn of the arithmetic seriesa1=22 d=-8 n=12

Answer 1

Given: An arithmetic series with:

`\begin{gathered} a_1=22 \\ d=-8 \\ n=12 \end{gathered}`

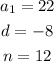
Required: To find the sum of n terms of the given series.

Explanation: The formula for the sum of n terms of an AP is:

`S_n=(n)/(2)[2a_1+(n-1)d]`

Substituting the values in the above formula gives:

`S_n=(12)/(2)[2*22+(12-1)\cdot(-8)]`

Solving the above equation-

`\begin{gathered} S_n=6(44-88) \\ S_n=-264 \end{gathered}`

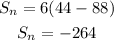
Final Answer: The sum of the arithmetic series is -264.