Given:
a,) The half-life of iodine-131 is 8 days.
b.) A hospital receives a shipment of 200 grams.
c.) Determine how much would remain after 32 days.
We will be using the following formula:
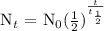
Where,

We get,
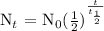
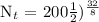
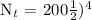
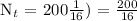
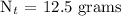
Therefore, in 32 days, only 12.5 grams of Iodine-131 will remain.