Let x be the liters need of the 25% acid solution, and y be the 70% acid solution, then we can set the following system of equations:
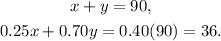
Solving the first equation for x, we get:
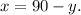
Substituting the above equation in the second equation we get:
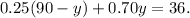
Simplifying and adding like terms we get:
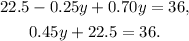
Adding 22.5 and then dividing by 0.45 we get:
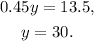
Substituting y=30 in x=90-y, we get:
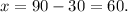
Therefore, x=60 liters, and y=30 liters.
Answer: 60 liters of the 25% acid solution are needed and 30 liters are needed of the 70% acid solution.