Question

How many liters each of a 25 % acid solution and a 70 % acid solution must be used to produce 90 liters of a 40 %acid solution? (Round to two decimal places if necessary.)

Answer 1

Let x be the liters need of the 25% acid solution, and y be the 70% acid solution, then we can set the following system of equations:

`\begin{gathered} x+y=90, \\ 0.25x+0.70y=0.40(90)=36. \end{gathered}`

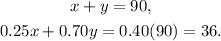
Solving the first equation for x, we get:

`x=90-y\text{.}`

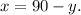
Substituting the above equation in the second equation we get:

`0.25(90-y)+0.70y=36.`

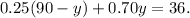
Simplifying and adding like terms we get:

`\begin{gathered} 22.5-0.25y+0.70y=36, \\ 0.45y+22.5=36. \end{gathered}`

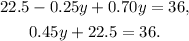
Adding 22.5 and then dividing by 0.45 we get:

`\begin{gathered} 0.45y=13.5, \\ y=30. \end{gathered}`

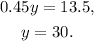
Substituting y=30 in x=90-y, we get:

`x=90-30=60.`

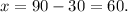
Therefore, x=60 liters, and y=30 liters.

Answer: 60 liters of the 25% acid solution are needed and 30 liters are needed of the 70% acid solution.