Question

Functions f(x) and g(x) are shown:f(x) = x2g(x) = x2 + 8x + 16In which direction and by how many units should f(x) be shifted to match g(x)?

Answer 1

we have the functions

`\begin{gathered} f(x)=x^2 \\ g(x)=x^2+8x+16 \end{gathered}`

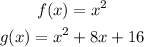
The vertex of function f(x) is the origin (0,0)

so

Find out the vertex of the function g(x)

Convert to vertex form

Complete the square

`\begin{gathered} g(x)=(x^2+8x)+16 \\ g(x)=(x^2+8x+4^2)+16-4^2 \\ g(x)=(x+4)^2 \end{gathered}`

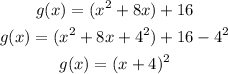
The vertex of the function g(x) is (-4,0)

therefore

The rule of the translation is given by

(x,y) -------> (x-4,y)

the translation should be 4 units to the left