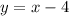In order to ginde the line equation for each line, we need to choose two points in each part.
Case 1. Left line (purple)
In this case, we can choose the points
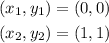
then the slope is given by
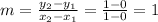
So, we have the following equation

where b is the y-intercept. We can find b by substituting in the last result one of the 2 given points. For instance, if we substitute point (0,0), we have
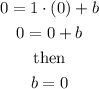
Therefore, the line equation for the purple line is:

Case 2. Center line (red)
Similarly to the previous case, we need to choose two points along the line, for instance
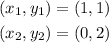
then, by applying the slope formula again, we have
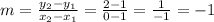
so, the red line has the form
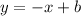
Again, we can find the y-intercept b by substituting one of the 2 given points. If we choose point (0,2), we get

Therefore, the equation of the center line (red) is given by:
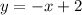
Case 3. Blue line
Again, we need to choose 2 points along the line, for instance,
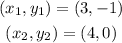
By substituting these point into the slope formula, we have
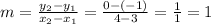
So, the line has the form
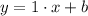
and by substituting the values of the point (4,0) into this equation, we have
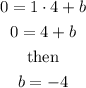
So, the equation of the right line (blue) is given by: