Question

A bag contains 8 red balls and 3 blue balls. Two balls are drawn at random one after the other without replacement. Find the probability that the balls drawn are red.

Answer 1

First, we need to calculate the probability of drawing a red ball the first time. This is given by the usual probability:

`P_{\text{red}1}=\frac{\text{red }}{total}=(8)/(11)`

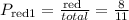
Now, as for the second time we pick a ball. Notice that the number of balls in the bag has changed since there is 1 red ball less. So, the probability of extracting a red ball under these conditions is:

`P_{\text{red}2}=\frac{red}{\text{total}}=(7)/(10)`

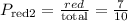
Notice that now the total number of balls is 10 and there are 7 red ones.

Finally, the probability we are looking for is given below:

`P_{\text{red}1}\cdot P_{\text{red}2}=(8)/(11)\cdot(7)/(10)=(56)/(110)\approx0.50909\ldots\approx0.51`

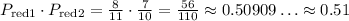
The probability is the above expression, in case you need it expressed as a fraction or a decimal number.