Question

What is the horizontal shift as well as the horizontal stretch/shrink of the function t(x)=4 cos((pi/12)x)+8?

Answer 1

Step-by-step explanation:

We were given the function:

`t\left(x\right)=4cos\left(\left((\pi)/(12)\right)x\right)+8`

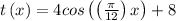
Graphically:

We are to determine its horizontal shift & its stretch/shrink. This is shown below:

Horizontal Shift:

`\begin{gathered} \text{From the general form of the sinusoidal function, we have:} \\ y=A\cos[B(x-C)]+D \\ where: \\ A=amplitude \\ (2\pi)/(B)=period \\ C=Phase(horizontal)\text{ }shift \\ D=Vertical\text{ }shift \end{gathered}`

Comparing the general form with the function given unto us, we have:

`C=0`

There is no horizontal shift

Horizontal stretch/shrink:

If we have: