Question

I need help understanding these concepts I know that the degree is 9 but don’t remember how to do the rest

Answer 1

Given:

`P(x)=x^9+2x^5-7x^3-x+2`

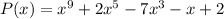
b) The polynomial of degree n has a total n linear factor.

The degree of the given polynomial is 9.

So, the linear factors are 9.

c) The number of real solutions is,

The positive real root

`\begin{gathered} P(x)=x^9+2x^5-7x^3-x+2 \\ \text{Changes the sign 2 times } \\ \text{from }+2x^5\text{ to }-7x\text{ and from }-x\text{ to }+2 \end{gathered}`

So, 2 positive real roots.

The negative real root,

`\begin{gathered} P(-x)=(-x)^9+2(-x)^5-7(-x)^3-(-x)+2 \\ =-x^9-2x^5+7x^3+x+2 \\ \text{Chnages the sign 1 times} \\ \text{from }-2x^5\text{ to }+7x^3 \end{gathered}`

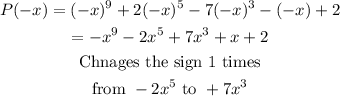
So, 1 negative rel root.

Hence the number of real solutions is 3.

d) As the total number of real solutions is 3. it means the polynomial can have 6 ( 9-3=6 ) or 0 number of complex solutions.

e) The fundamental theorem of algebra can be used to determine the complex solutions of the polynomial.

f) To check x = 2 is the solution of the given polynomial or not.

`\begin{gathered} P(x)=x^9+2x^5-7x^3-x+2 \\ \text{for x=2} \\ P(2)=2^9+2(2)^5-7(2)^3-2+2=520\\e0 \\ \Rightarrow x=2\text{ is not the solution of the given polynomial} \end{gathered}`

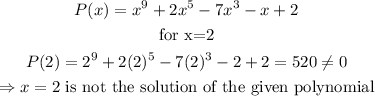
x=2 is not the solution of the given polynomial as it does not satisfy f(2)=0.