Question

Triangle RST is translated along the indicated vector to create the image R'S'T'. What are the coordinates of the vertices of the image?If R and R' are connected with a straight line, the line segment RR' would measure_____units

Answer 1

(a)R'(5,5), S'(9.2) and T'(4,2)

(b)5 units.

Step-by-step explanation:

The indicated vector shows a translation of 4 units down and 3 units right.

From the graph, the vertices of triangle RST are:

R(2,9), S(6, 6) and T(1,6)

(a)The coordinates of the vertices of the image will then be:

`\begin{gathered} R^(\prime)=(2+3,9-4)=(5,5) \\ S^(\prime)=(6+3,6-4)=(9,2) \\ T^(\prime)=(1+3,6-4)=(4,2) \end{gathered}`

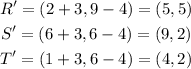
(b)If R and R' are connected with a straight line

The length of the line segment RR' will be the distance between R(2,9) and R'(5,5).

Using the distance formula, we have:

`\begin{gathered} Distance=√((x_2-x_1)^2+(y_2-y_1)^2) \\ =\sqrt[]{(2-5)^2+(9-5)^2} \\ =\sqrt[]{(-3)^2+(4)^2} \\ =\sqrt[]{25} \\ =5\text{ units} \end{gathered}`

The line segment RR' would measure 5 units.