Question

A light ray enters a square block of plastic at an angle 1 = 54° (measured from the surface normal) and emerges at an angle 2 = 67° (measured from its surface normal) as shown. The light ray enters the plastic a distance = 75 above the corner and emerges a distance from the corner.What is the index of refraction of the plastic? (Assume air is the surrounding medium, with an index of refraction of 1.00.)What is , in centimeters?

Answer 1

Let θ be the angle from the normal to the surface to the ray of light inside the block after the first refraction:

Let n_1 be the index of refraction that corresponds to the medium of the angle θ_1. According to Snell's Law:

`\begin{gathered} n_1\sin (\theta_1)=n\sin (\theta) \\ n\sin (90-\theta)=n_2\sin (\theta_2) \end{gathered}`

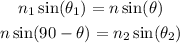
Since the angles θ_1 and θ_2 correspond to the air, then n_1=1 and n_2=1, Then:

`\begin{gathered} \sin (\theta_1)=n\sin (\theta) \\ n\sin (90-\theta)=\sin (\theta_2) \end{gathered}`

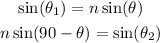
Since sin(90-θ)=cos(θ), then:

`n\cos (\theta)=\sin (\theta_2)`

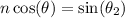
Isolate sin(θ) and cos(θ) from their corresponding equations:

`\begin{gathered} \sin (\theta)=\frac{\sin(\theta_1)_{}}{n} \\ \cos (\theta)=(\sin(\theta_2))/(n) \end{gathered}`

Recall the Pythagorean Identity:

`\sin ^2(\theta)+\cos ^2(\theta)=1`

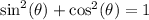
Replace the expressions for sin(θ) and cos(θ):

`\begin{gathered} ((\sin (\theta_1))/(n))^2+((\sin (\theta_2))/(n))^2=1 \\ \Rightarrow(\sin^2(\theta_1))/(n^2)+(\sin ^2(\theta_2))/(n^2)=1 \\ \Rightarrow\sin ^2(\theta_1)+\sin ^2(\theta_2)=n^2 \\ \Rightarrow\sqrt[]{\sin ^2(\theta_1)+\sin ^2(\theta_2)}=n \end{gathered}`

Therefore, the index of refraction is given by:

`n=\sqrt[]{\sin^2(\theta_1)+\sin^2(\theta_2)}`

Substitute θ_1=54° and θ_2=67° to find the index of refraction of the material:

`\begin{gathered} n=\sqrt[]{\sin^2(54)+\sin^2(67)} \\ =1.22549\ldots \\ \approx1.23 \end{gathered}`

From the diagram, notice that:

`\begin{gathered} \tan \theta=(L)/(X) \\ \Rightarrow X=(L)/(\tan \theta) \end{gathered}`

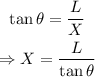
On the other hand:

`\tan (\theta)=(\sin (\theta))/(\cos (\theta))`

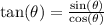
Substitute the expressions for sin(θ) and cos(θ):

`\begin{gathered} \tan (\theta)=\frac{(\frac{\sin(\theta_1)_{}}{n})}{(\frac{\sin(\theta_2)_{}}{n})} \\ =(\sin(\theta_1))/(\sin(\theta_2)) \end{gathered}`

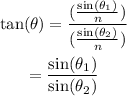
Substitute the expression for tan(θ) into the formula to find X:

`\begin{gathered} X=(L)/(((\sin(\theta_1))/(\sin(\theta_2)))) \\ =(\sin (\theta_2))/(\sin (\theta_1))L \end{gathered}`

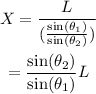
Substitute L=75cm, θ_1=54° and θ_2=67° to find the value of X:

Therefore, the answers are: