Question

Need more explanation to this review question. Not understanding what it wants me to find.

Answer 1

We need to write an equation relating x (leg CD) to the given data.

The image shows the right triangle ACD, with legs, in ft, given by:

`\begin{gathered} AC=1600 \\ \\ CD=x \end{gathered}`

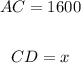
Also, angle DAC is 25.4º. Since CD is the opposite leg, and AC is the adjacent leg to this angle, we have:

`\begin{gathered} \tan 25.4\degree=(CD)/(AC) \\ \\ \tan 25.4\degree=(x)/(1600) \end{gathered}`

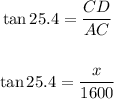
Thus, option A is correct.

Also, we can multiply both sides of the above equation by 1600, to find the equivalent equation:

`\begin{gathered} 1600\cdot\tan 25.4\degree=(x)/(1600)\cdot1600 \\ \\ 1600\cdot\tan 25.4\degree=x \\ \\ x=1600\cdot\tan 25.4\degree \end{gathered}`

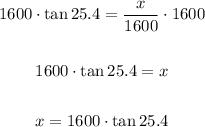
Thus, option C is also correct.

Notice that:

`\begin{gathered} \cos 25.4\degree=(AC)/(AD) \\ \\ \cos 25.4\degree=\frac{1600^2^{}+x^2}{1600} \end{gathered}`

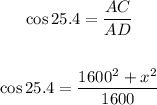
Therefore, only options A and C are correct.