Question

Saw the rational inequality Express your answer in interval notation

Answer 1

To solve a rational inequality we need to remember that, in the real numbers, when we multiply an inequality by a number the order of the inequality is preserved only if the number we are multiplying is positive. This means that we need to be careful with the sign of the denominators and for this reason we need to solve the inequality considering all possible cases.

Case 1.

In this case we will assume that:

`\begin{gathered} x+3>0 \\ x-3>0 \end{gathered}`

This means that both denominators are positive and we can multiply them in both sides and the order will be preserved, then we have:

`\begin{gathered} (x-2)(x-3)\leq x(x+3) \\ x^2-5x+6\leq x^2+3x \\ x^2+3x-x^2+5x\ge6 \\ 8x\ge6 \\ x\ge(6)/(8) \\ x\ge(3)/(4) \end{gathered}`

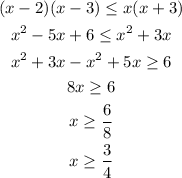
Now we need to find the intersection of the condition we stated above for the denominators and the solution we found; by doing this we conclude that the solution for this case is the interval:

`(3,\infty)`

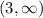
Case 2:

In this case we will assume that:

`\begin{gathered} x+3>0 \\ x-3<0 \end{gathered}`

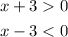
Then we have:

`\begin{gathered} (x-2)(x-3)\ge x(x+3) \\ x^2-5x+6\ge x^2+3x \\ x^2+3x-x^2+5x\leq6 \\ 8x\leq6 \\ x\leq(6)/(8) \\ x\leq(3)/(4) \end{gathered}`

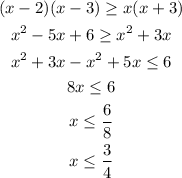
Then we have the solution:

`(-3,(3)/(4)\rbrack`

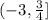
Case 3:

In this case we will assume that:

`\begin{gathered} x+3<0 \\ x-3>0 \end{gathered}`

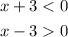
Then we have:

`\begin{gathered} (x-2)(x-3)\ge x(x+3) \\ x^2-5x+6\ge x^2+3x \\ x^2+3x-x^2+5x\leq6 \\ 8x\leq6 \\ x\leq(6)/(8) \\ x\leq(3)/(4) \end{gathered}`

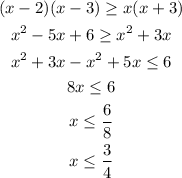
In this case we don't have any intersection among our three conditions and hence this case does not have a solution.

Case 4:

In this case we will assume that:

`\begin{gathered} x+3<0 \\ x-3<0 \end{gathered}`

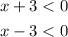
Then we have:

`\begin{gathered} (x-2)(x-3)\leq x(x+3) \\ x^2-5x+6\leq x^2+3x \\ x^2+3x-x^2+5x\ge6 \\ 8x\ge6 \\ x\ge(6)/(8) \\ x\ge(3)/(4) \end{gathered}`

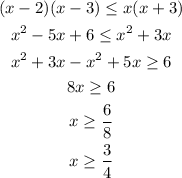
In this case we don't have any intersection among our three conditions and hence this case does not have a solution.

Finally we take the union of the solutions we found. Therefore, the solution of the inequality is:

`(-3,(3)/(4)\rbrack\cup(3,\infty)`