Since we want to specify the length of the sides of a triangle from the known lengths of another triangle that is similar to the first one, we can express the ratios of their sides like this:
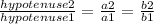
Where 1 means triangle 1, 2 means triangle 2, a is the first leg and b is the other leg.
Replacing the values that we know from the triangle one we get:
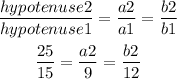
Now, let's find the length of the second triangle with the first two ratios, like this:
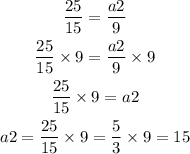
And for the second length of the second triangle we can use the first and the last ratio, like this:
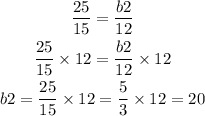
Then the second triangle has two legs of length 15 and 20