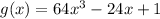By the rules of transformation of functions, you know that
*f(bx), where b>1, the function shrinks the curve horizontally by a factor of b.
*f(x)+k moves the function k units up
So, in this case, you have
*b=4 and
*k=2

To verify you can graph the functions f(x) and g(x), like this
Therefore, the function g(x) is