Question

A Sno-Cone at the carnival has the shape of a hemisphere on top of an inverted cone. What is the volume ofthe sno-cone if its radius is 4.2 yd and the height of the conical portion is 8.3 yd?

Answer 1

The given diagram consists of two parts, a cone and a hemisphere.

The total volume of the solid will be equal to the sum of the volumes of cone and hemisphere.

Note that the both the parts share the same circular base, so the radius of the sphere will be the same as the radius of base of the cone.

According to the given data, the radius (r) of circular base is 4.2 yd, and the height (h) of the cone is 8.3 yd.

The volume of the Hemispherical part is calculated as,

`\begin{gathered} V_h=(4)/(3)\pi R^3 \\ V_h=(4)/(3)\pi(4.2)^3 \\ V_h=98.784\pi \end{gathered}`

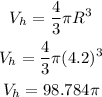
And the volume of cone is calculated as,

`\begin{gathered} V_c=(1)/(3)\pi R^2h \\ V_c=(1)/(3)\pi(4.2)^2(8.3) \\ V_c=48.804\pi \end{gathered}`

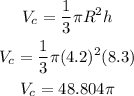
Now, the total volume of the solid (V) is given by,

`\begin{gathered} V=V_h+V_c \\ V=98.784\pi+48.804\pi \\ V=147.588\pi \\ V\approx463.66 \end{gathered}`

Thus, the volume of the given Sno-Cone is approximately 463.66 cubic yards.