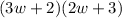Question

Completely factor the trinomial, if possible6w^2+13w+6

Answer 1

Given the expression in the question tab, the following solution steps completely factorize the trinomial expression.

Step 1: Write out the trinomial

`6w^2+13w+6`

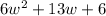
Step 2: Factorize using the fatorization method

`\begin{gathered} 6w^2+13w+6-----\text{equation 1} \\ \text{ multiply the constant by the coefficient of w}^2 \\ we\text{ have }36w^2 \\ we\text{ find two factors of 36w}^2\text{ that can sum up to give 13w} \\ \text{The factors are }9w\text{ and }4w \\ \text{Substituting these factors for 13w in equation 1, we have:} \\ 6w^2+9w+4w+6 \\ By\text{ factorization, we have:} \\ 3w(2w+3)+2(2w+3) \\ (3w+2)(2w+3) \end{gathered}`

Therefore, the factors of the trinomial expression are:

`(3w+2)(2w+3)`