Question

The explicit rule for a sequence and one of the specific terms is given. Find the position of the given term.

Answer 1

Given:

The explicit rule for a sequence is given as:

`f(x)=1.25n+6.25`

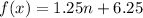
The given specific term is 25.

The aim is to find the position of the term 25.

The position of the term 25 is given by the value of n when f(n)= 25.

Therefore,

`\begin{gathered} f(n)=25 \\ 1.25n+6.25=25 \\ 1.25n=25-6.25 \end{gathered}`

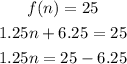
Solving further,

`\begin{gathered} 1.25n=18.75 \\ n=(18.75)/(1.25) \\ n=15 \end{gathered}`

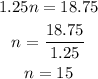
Hence, the position of term 25 is 15.