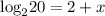Question

If log2 5=x and log2 3=y, determine log2 20 can you help me learn how to do this?

Answer 1

2+x

Step-by-step explanation:

Given the following:

`\begin{gathered} \log _25=x \\ \log _23=y \end{gathered}`

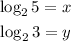
The idea is to express the given integer (20) in terms of either the base or the values given (3 and 5).

`\begin{gathered} \log _220=\log _2(4*5) \\ =\log _2(2^2*5) \end{gathered}`

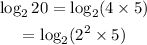
Next, since we have the multiplication sign, we use the addition law:

`=\log _22^2+\log _25`

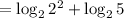
The power of the number becomes the product of the log, so we have:

`=2\log _22+\log _25`

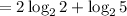
When you have the same base and number, the result is always 1.

`\begin{gathered} \log _22=1 \\ \implies2\log _22+\log _25=2(1)+\log _25 \\ =2+x \end{gathered}`

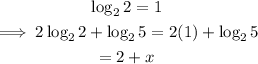
Therefore:

`\text{log}_220=2+x`