Question

3. Natasha places a mirror on the ground 24 ft from the base of an oak tree. She walks backward until she can see the top of the tree in the middle of the mirror. At that point, Natasha's eyes are 5.5 ft above the ground, and her feet are 4 ft from the image in the mirror Find the height of the oak tree,

Answer 1

The figure for the Natasha height and height of tree can be draw as,

The length MO is 4ft.

The length of MQ is 24 feet.

The length of NO is 5.5 ft.

The length of tree (PQ) is x.

Consider the triangle MNO and triangle MPQ.

`\begin{gathered} \angle NMO\cong\angle PMQ \\ \angle NOM\cong\angle PQM\text{ (Each right angle)} \\ \Delta NOM\cong\Delta PQM\text{ (By AA similarity)} \end{gathered}`

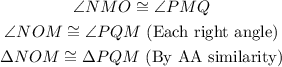
For similar triangle ratio of sides are equal. So,

`\begin{gathered} (NO)/(PQ)=(MO)/(MQ) \\ (5.5)/(x)=(4)/(24) \\ (5.5)/(x)=(1)/(6) \\ x=5.5\cdot6 \\ =33 \end{gathered}`

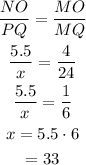
Thus height of oak tree is 33 ft.