Given:
Volume of cylinder, V = 90π cm³
Radius, r = 3 cm
Let's find the height of the cylinder.
To find the height, given the volume, apply the formula for the volume of a cylinder:
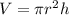
Where h is the height.
Let's rewrite the formula for h to solve for h.
Re-arrange the equation:
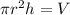
Divide both sides by πr²:
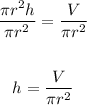
Now, substitute values into the equation and solve for h.
Where:
V = 90π
r = 3
We have:
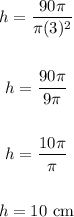
Therefore, the height of the cylinder is 10 cm.
ANSWER:
D. 10 cm