Step-by-step explanation
Since we have the table with the values of x and y, we can draw the graph as show as follows:
The rate of change can be computed by taking two given points and calculating the slope as shown as follows:
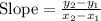
As we have (x_1,y_1) = (1,13) and (x_2,y_2) = (3,39), substituting terms:
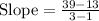
Subtracting numbers:
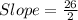
Simplifying:
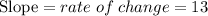
The constant rate of change is 13
The function is linear because we have a constant rate of change and the form of the graph is a line.