Question

The midpoint of PQ is M=(1, -5) . One endpoint is P=(6, -8).Find the coordinates of the other endpoint, Q.

Answer 1

Given:

The midpoint of a line PQ is M = (1,-5).

THe coordinate of point P = (6,-8).

The objective is to find the coordinate of other point Q.

Step-by-step explanation:

Since, M is the midpoint of PQ, the distance between PM and QM will be equal.

Consider the coordinate of P , M and Q as,

`\begin{gathered} P(x_1,y_1)=P(6,-8) \\ M(x,y)=(1,-5) \\ Q\mleft(x_2,y_2\mright) \end{gathered}`

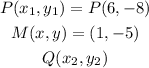
The general midpoint formula is,

`\begin{gathered} M=((x_1+x_2)/(2),(y_1+y_2)/(2)) \\ (x,y)=((x_1+x_2)/(2),(y_1+y_2)/(2)) \end{gathered}`

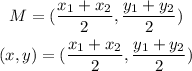
To find the value of x value of point Q:

By equating only the variables of x,

`\begin{gathered} x=(x_1+x_2)/(2) \\ 1=(6+x_2)/(2) \\ 1(2)=6+x_2_{} \\ x_2=2-6 \\ x_2=-4 \end{gathered}`

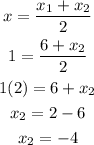
To find the value of y value of point Q:

By equating only the variable of y,

`\begin{gathered} y=(y_1+y_2)/(2) \\ -5=(-8+y_2)/(2) \\ -5(2)=-8+y_2 \\ y_2=-10+8 \\ y_2=-2 \end{gathered}`

Hence, the coordinate of Q is (-4,-2).