Given:
Adult ticket cost = $10
Student ticket cost = $6
Total people = 750 people
Total amount = $6860
Find-:
How many of each type of ticket were sold
Explanation-:
Let student is "x."
The adult is "y."
The total people is 750 people,
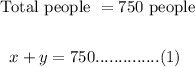
The total amount is $6860
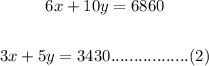
Solve the equation is:
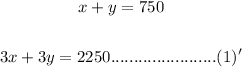
Then eq(2) - eq(1)' then value of "y" is:
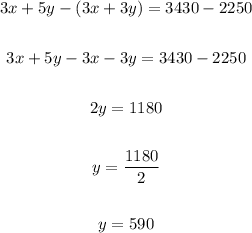
Adult member is 590
Student ticket is:
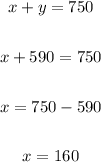
The number of students is 160.