Given data:
![F(x)=\sqrt[3]{x-2}+3](https://img.qammunity.org/2023/formulas/mathematics/college/43381ff9r0n6k5oord6cnhz069j2e53gej.png)
A. The domain of cube root function is all the real numbers because it is possible for three negatives to equal a negative. But this cannot apply for square functions.
B. For range put F(x) = y
![\begin{gathered} y=\sqrt[3]{x-2}+3 \\ y-3=\sqrt[3]{x-2} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/r9tkv5sdq5fhevejm3k93ilr1l6kyv8h94.png)
Now, taking cube both sides we get
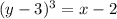
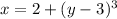
Thus, the range for the function is also all real numbers because value of x will be defined for every value of y.