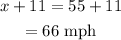Question

Question 5 of 10, Step 1 of 13/10CorrectJustin recently drove to visit his parents who live 240 miles away. On his way there his average speed was 11 miles per hour faster than on his way home (he ran intosome bad weather). If Justin spent a total of 8 hours driving find the two rates.

Answer 1

Given,

The distance, D = 240 miles

The average speed was 11 miles per hour.

Solution:

Let x be the speed.

Then, (x+11) will be the average speed.

The time taken to cover outward bound is

`Time=(240)/(\left(x+11\right))hrs......\lparen1)`

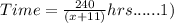
The time taken to cover homeward bound is

`Time=(240)/(x)\text{ hrs......\lparen2\rparen}`

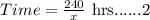
Add both equations (1) and (2)

`\begin{gathered} Time\text{ + Time = 8 hrs} \\ (240)/(\left(x+11\right))+(240)/(x)=8 \\ (240x+240\left(x+11\right))/(x\left(x+11\right))=8 \\ (240x+240x+2,640)/(x\left(x+11\right))=8 \end{gathered}`
`\begin{gathered} 480x+2640=8\lparen x^2+11x) \\ 480x+2640=8x^2+88x \\ 8x^2+88x-480x-2640=0 \\ 8x^2-392x-2640=0 \end{gathered}`

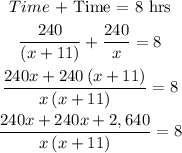
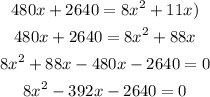
Divide the equation by 5.

`\begin{gathered} x^2-49x-330=0 \\ x^2+6x-55x-330=0 \\ x\left(x+6\right)-55\left(x+6\right)=0 \\ \lparen x+6)\left(x-55\right)=0 \end{gathered}`

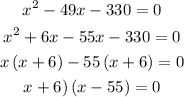
Thus, the value of x is

`x=55,-6`

Justin's average speed to his parents house is 55 mph.

Justin's average speed from his parent's house is

`\begin{gathered} x+11=55+11 \\ =66\text{ mph} \end{gathered}`