Answer:
The inequality is given below as
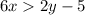
Step 1:
Concept:
The slope-intercept form is given below as
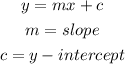
To put the inequality in slope-intercept form, we will make y the subject of the formula
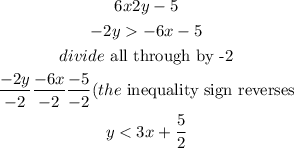
Hence,
By rearranging it in slope-intercept form, we will have the inequality be
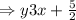
Step 2:
Describe the type of boundary lines to be used
Boundary lines in math are the same: they identify the outer edge (or outline) of a shape or area. This could be a geometric shape or an inequality graph.
The graph of an inequality in two variables is the set of points that represents all solutions to the inequality. A linear inequality divides the coordinate plane into two halves by a boundary line where one half represents the solutions of the inequality. The boundary line is dashed for > and < and solid for ≤ and ≥.
Hence,
The boundary line to be used will be DASHED
Step 3:
Determine where to be shaded
The inequality in slope-intercept form is given below as
![\operatorname{\Rightarrow}y\lt3x+(5)/(2)]()
Shade the appropriate region. Unless you are graphing a vertical line the sign of the inequality will let you know which half-plane to shade. If the symbol ≥ or > is used, shade above the line. If the symbol ≤ or < is used shade below the line.
Graphically,
Hence,
The sign used in the inequality here is <.
Therefore,
We will have to SHADE BELOW THE LINE