Question

Arrange the following inequality into slope-intercept form. Then describe what type of boundary line would be used.

Answer 1

The inequality is given below as

`6x>2y-5`

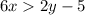
Step 1:

Concept:

The slope-intercept form is given below as

`\begin{gathered} y=mx+c \\ m=slope \\ c=y-intercept \end{gathered}`

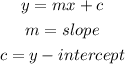
To put the inequality in slope-intercept form, we will make y the subject of the formula

`\begin{gathered} 6x\gt2y-5 \\ -2y>-6x-5 \\ divide\text{ all through by -2} \\ (-2y)/(-2)\gt(-6x)/(-2)(-5)/(-2)(the\text{ inequality sign reverses\rparen} \\ y<3x+(5)/(2) \end{gathered}`

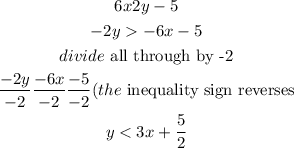
Hence,

By rearranging it in slope-intercept form, we will have the inequality be

`\Rightarrow y\lt3x+(5)/(2)`

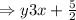
Step 2:

Describe the type of boundary lines to be used

Boundary lines in math are the same: they identify the outer edge (or outline) of a shape or area. This could be a geometric shape or an inequality graph.

The graph of an inequality in two variables is the set of points that represents all solutions to the inequality. A linear inequality divides the coordinate plane into two halves by a boundary line where one half represents the solutions of the inequality. The boundary line is dashed for > and < and solid for ≤ and ≥.

Hence,

The boundary line to be used will be DASHED

Step 3:

Determine where to be shaded

The inequality in slope-intercept form is given below as

Shade the appropriate region. Unless you are graphing a vertical line the sign of the inequality will let you know which half-plane to shade. If the symbol ≥ or > is used, shade above the line. If the symbol ≤ or < is used shade below the line.

Graphically,

Hence,

The sign used in the inequality here is <.

Therefore,

We will have to SHADE BELOW THE LINE