ANSWER:
100%
Explanation:
The first thing is to extract the sample spaces of the events, just like this:
A (even number) = {2, 4, 6, 8, 10, 12, 14}
B (multiple of 4) = {4, 8, 12}
A n B = {4, 8, 12}
Now, we calculate the probability of each case
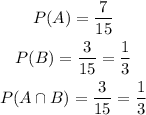
We have that the probability P (A | B) is calculated as follows:
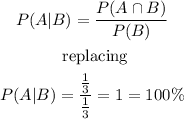
The probability is 100% since every multiple of 4 is even.