Question

2. (08.01 MC)A cone has a volume of 5 cubic inches. What is the volume of a cylinder that the cone fits exactly inside of? (1 point)15 in^320 in^325 in^3 30 in^3

Answer 1

According to the information given in the exercise, the volume of a cone is:

`V_(co)=5in^3`

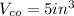
You need to remember that:

- The formula for calculating the volume of a cone is:

`V_(co)=(\pi r^2h)/(3)`

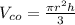
Where "r" is the radius and "h" is the height.

- The formula for calculating the volume of a cylinder is:

`V_(cy)=\pi r^2h`

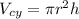
Where "r" is the radius and "h" is the height of the cylinder.

In this case, you know that the cone fits exactly inside of the cylinder. That indicates that the height and the radius of both solids are equal.

Then to find the volume of the cylinder, you need to:

1. Substitute the volume of the cone into the formula for calculating the volume of a cone:

`5in^3=(\pi r^2h)/(3)`

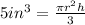
2. Solve for:

`\pi r^2h`

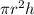
Then, you get:

`\begin{gathered} (3)(5in^3)=\pi r^2h \\ \\ 15^{}in^3=\pi r^2h \end{gathered}`

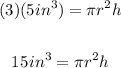
3. Substitute that value into the formula for calculating the volume of a cylinder:

`V_(cy)=15in^3`

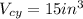
Hence, the answer is: First option.