Question

-12x+6y=-12 graph Please help with equation

Answer 1

In ths problem, we need to graph a linear equation in standard form: ax + by = c

The easiest way to do this is to use the x-intercept and y-intercept:

- x-intercept, where the graph crosses the x-axis when y = 0

- y-intercept, where the graph crosses the y-axis when x = 0

We are given the equation

`-12x+6y=-12`

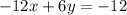
To find the x-intercept, we will let y = 0, then solve for x. So,

`\begin{gathered} -12x+6(0)=-12 \\ -12x=-12 \end{gathered}`

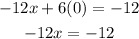
Divide by -12 on both sides:

`\begin{gathered} (-12)/(-12)x=(-12)/(-12) \\ \\ x=1 \end{gathered}`

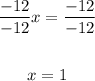
The x-intercept is at x = 1, so the point we can graph is (1,0):

Next, we can find the y-intercept by letting x = 0. That gives us:

`\begin{gathered} -12(0)+6y=-12 \\ \\ 6y=-12 \end{gathered}`

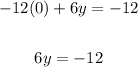
Divide both sides by 6:

`\begin{gathered} (6y)/(6)=-(12)/(6) \\ \\ y=-2 \end{gathered}`

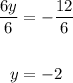
So the y-intercept is y = -2 at the point (0,-2). We can graph that point next:

Finally, we can u