Since the relationship is linear, we will solve it as follows:
*We are given two points, we will find the slope:
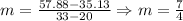
*Now, we replace this slope and one of the points in the following expression:

Now, we replace:
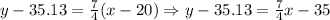
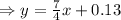
Now, we replace the 27 HCF in the expression and solve for the cost:
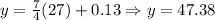
So, the cost for 27 HCF is $47.38.