Question

Find the volume of a square pyramid with a perimeter of 56 inches and a slant height of 25 inches.

Answer 1

The volume of a square pyramid is

`V=(1)/(3)\cdot a^2\cdot h`

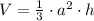
Where a is the length of each base side.

First, we have to find a using the perimeter.

`\begin{gathered} P=4a \\ 56in=4a \\ a=(56in)/(4) \\ a=14in \end{gathered}`

Then, we find h using Pythagorean's Theorem,

`c^2=a^2+b^2`

Where c = 25in, b = 7in, and a represents the height h

`\begin{gathered} (25in)^2=h^2+(7in)^2 \\ 625in^2=h^2+49in^2 \\ h^2=625in^2-49in^2 \\ h=\sqrt[]{576in^2} \\ h=24in \end{gathered}`

Now, we find the volume

`\begin{gathered} V=(1)/(3)\cdot(14in)^2\cdot24in \\ V=(1)/(3)\cdot196in^2\cdot24in \\ V=1,568in^3 \end{gathered}`

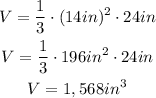
Hence, the volume of the square pyramid is 1,568 cubic inches.