Question

The height of a houseplant is normally distributed with a mean of 12 inches and a standard deviation of 2 inches. Using the empirical rule, what is the probability that a houseplant will be longer than 16 inches? a0.975 b0.95 c0.05 d0.025

Answer 1

From the information given:

`\begin{gathered} mean,\text{ }\mu=12\text{ inches} \\ Standard\text{ deviation, }\sigma=2\text{ inches} \\ sample,\text{ x = 16} \end{gathered}`

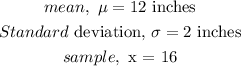
Calculate the z-score

`z=(x-\mu)/(\sigma)=(16-12)/(2)=(4)/(2)=2`

The empirical state as shown below

We can see in the illustration above that population within 2 standard deviation is 95% (i.e 0.95).

However, The question says to find the probability that a houseplant will be longer than 16 inches, that is above 2 standard deviation from our calculation

This gives 1-0.95 = 0.05