Question

Hello can someone please try to explain this to me as simply as possible

Answer 1

The easiest way to solve this problem is to substract 2π from the angle until we get an angle that is less than 2π.

`(19)/(3)\pi-2\pi=(19-6)/(3)\pi=(13)/(3)\pi`

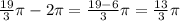
13/3π is not less than 2π, so we have to substract 2π once more:

`(13)/(3)\pi-2\pi=(13-6)/(3)\pi=(7)/(3)\pi`

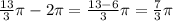
7/3π is still not less than 2π, substract 2π once more:

`(7)/(3)\pi-2\pi=(7-6)/(3)\pi=(1)/(3)\pi`

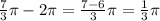
1/3π is less than 2π. It means that the positive angle less than 2π that is coterminal with 19/3π is 1/3π.