Explanation:
Step 1. We have a piecewise function defined for certain x value intervals.
for x values between -4 and -1, the definition is:
![f(x)=x+6,\text{ for }-4And for the x values between -1 and 5, the definition is:[tex]f(x)=-2x+7,\text{ for }-1<strong>Step 2. </strong>We need to graph the function, for that, we start with the definition for x values between -4 and -1[tex]\begin{equation*} f(x)=x+6 \end{equation*}]()
To graph this, we compare it with the general line function
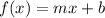
where m is the slope (the rate of change of the line) and b is the y-intercept. In this case, for f(x)=x+6, the slope is m=1, and the y-intercept is 6, if we were to graph this line in the whole plane, it would look as follows:
But since this is just the definition of the function for the values between -4 and -1, the result is:
Step 3. Now we consider the second definition of the function:

Comparing it with the general line function
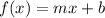
where m is the slope (the rate of change of the line) and b is the y-intercept.
Here in f(x)=-2x+7, the slope is m=-2, and the y-intercept is b=7, which means that the line is decreasing at a rate of -2, and that it crosses the y-axis at 7.
If we were to graph this line in the whole plane, it will look as follows (in blue):
But since that is the definition of the function only for the interval from -1 to 5, we only consider the line for that specific x-interval, we represent the point at -1 with an open circle and at 5 with a filled circle to represent that 5 is included in the segment:
Answer: