We know that Newton's law of cooling is:

From the problem we know that the cup was originally at 210°F and that the room is at 68°F, then we have:

To determine the value of k we use the fact that after 10 minutes the temperature of the object is 200°F, then we have:
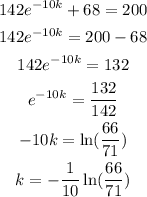
Then the temperature of the cup is decreasing according to the function:
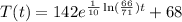
Now, that we have the function we can determine how much time it will take for the cup to be 180°F we equate our function to this temperature and solve for t:
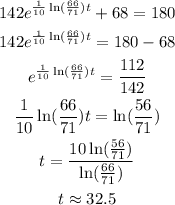
Therefore, it will take approximately 33 minutes for the cup to be 180°F