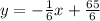Question

Find an equation of the line perpendicular to y=6x+4 that passes through the point (5,10) if possible write the equation in slope intercept form

Answer 1

Given:

y = 6x + 4

The slope of a perpendicular line, is the negative reciprocal of the slope of the original line.

Using the slope intercept form:

y = mx + b

Where m is the slope and b is the y-intercept

The slope of the origi line: y = 6x + 4 is = 6

The negative reciprocal of 6 is:

`-(1)/(6)`

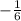
Thus, the slope of the perpendicular line is

`-(1)/(6)`

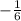
To find the equation of the perpendicular line that passes through the point (5, 10), use the slope-intercept form:

y = mx + b

Substitute -1/6 for m, 5 for x and 10 for y to find b.

We have:

`\begin{gathered} y=mx+b \\ \\ 10=-(1)/(6)\ast5+b \\ \\ 10=-(5)/(6)+b \\ \\ \text{Multiply through by 6:} \\ 10\ast6=-(5)/(6)\ast6+6b \\ \\ 60=-5+6b \\ \\ 60+5=-5+5+6b \\ \\ 65=6b \\ \\ (65)/(6)=b \end{gathered}`

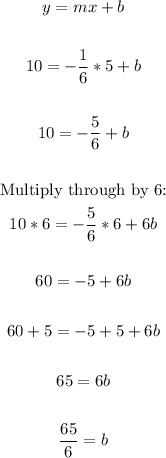
Therefore, the equation of the perperndicular line in slope intercept form is:

`y=-(1)/(6)x+(65)/(6)`

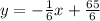
ANSWER:

`y=-(1)/(6)x+(65)/(6)`