Givens.
• The mass is 20 kg. (m = 20kg)
,
• The applied force is 63 N. (F = 63 N).
First, we have to make a free-body diagram to visualize the problem and its vectors.
Use Newton's Second Law for the horizontal vectors and vertical vectors.
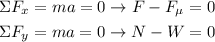
Use the equations for weight and friction force.
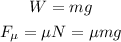
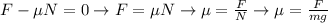
Where F = 65 N, m = 20kg, and g = 9.8 m/s^2.
![\begin{gathered} \mu=\frac{65N}{20\operatorname{kg}\cdot9.8((m)/(s^2))} \\ \mu=(65N)/(196N) \\ \mu\approx0.33 \end{gathered}]()
Therefore, the kinetic friction coefficient is 0.33.