We are given the following equation:
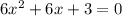
This is an equation of the form:
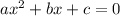
The discriminant of the equation is:
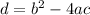
We have 3 possible cases:
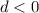
There are two imaginary solutions
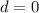
one real solution
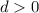
Two real solutions.
Replacing the values:
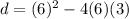
Solving the operations:
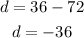
We have:
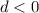
This means that we have 2 imaginary solutions.