The sine rule is used when we are given either
a) two angles and one side, or
b) two sides and a non-included angle.
The cosine rule is used when we are given either
a) three sides or
b) two sides and the included angle.
For the given problem, we are given a non-included angle and two sides. Hence, we have to solve the problem using the law of sines.
The sine rule states that:
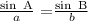
We have:
A = 35 degrees, b = 13, a = 11
Substituting we have:
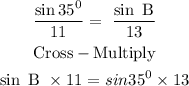
Divide both sides by 11 and solving for B:
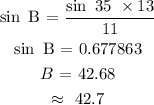
Using the property of triangles, we can find the angle C:
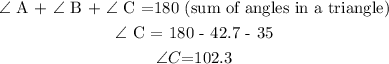
Using the sine rule, we can solve for the unknown side c. We have:
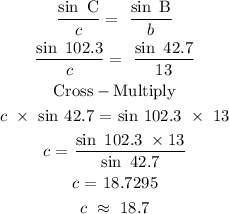
Answer summary
Law of Sines; B ≈ 42.7°, C ≈ 102.3°, c ≈ 18.7