Question

The common difference for a geometric sequence given by one negative negative 1 negative negative 3 negative 5 negative 7 is 2

Answer 1

-Given the sequence;

`1,-1,-3,-5,-7,\ldots`

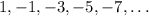
An arithmetic sequence is a sequence with a common difference;

A geometric sequence is a sequence with a common ratio.

In the above sequence, there is no common ratio but there is a common difference. Hence, the sequence is arithmetic.

The common difference d is;

`\begin{gathered} d=a_2-a_1=a_3-a_2 \\ d=-1-1=-3-(-1) \\ d=-2 \end{gathered}`

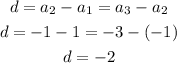
Thus, the statement "The common difference for the geometric sequence given by 1, -1, -3, -5, -7,.... is 2." is FALSE.

The correct statement is "The common difference for the arithmetic sequence given by 1, -1, -3, -5, -7,.... is -2.