Answer:
![\begin{gathered} x=-3-\sqrt[]{11} \\ x=\sqrt[]{11}-3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/yni6jeu1slobynvqu9ymjl6i25luh3gsmk.png)
Step-by-step explanation:
First we write our equation as
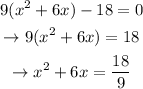
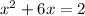
Now, adding 9 to both sides gives
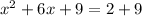
which lets us rewrite

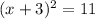
Taking the square root of both sides gives
![x+3=\pm\sqrt[]{11}](https://img.qammunity.org/2023/formulas/mathematics/college/8mf083ystuia3s5g0kjmdyoqlck7nertm6.png)
Subtracting 3 from both sides gives
![x=\pm\sqrt[]{11}-3](https://img.qammunity.org/2023/formulas/mathematics/college/dlzpeg0j0pmd7tzaadl4etprqvrwe7xlx3.png)
which gives us two solutions
![\begin{gathered} x=\sqrt[]{11}-3 \\ x=-\sqrt[]{11}-3 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/ykgya4dqz2im893z5xss65erow9cvz67hf.png)
which are our answers!