Question

You pick a card at random, put it back, and then pick another card at random.4567What is the probability of picking a 7 and then picking an even number?Write your answer as a percentage.

Answer 1

We have two picking rounds with replacement.

We have to calculate the probability of picking a 7 and then picking an even number.

As the picking is made with replacement, the probabilities of both events are independent.

Then, we can write:

`P(7\&E)=P(7)\cdot P(E)`

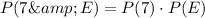
We can calculate the probability of each event as the quotient between the successful outcomes and the possible outcomes.

For the first event we have 1/4 as we have one successful event (getting a 7) out of 4 possible events.

For the second event we have 2/4 = 1/2, as we have two successful events (get a 4 or a 6) out of 4 possible events.

Then, we can calculate the probability as:

`P(7\&E)=P(7)\cdot P(E)=(1)/(4)\cdot(1)/(2)=(1)/(8)=0.125`

We can express this probability as a percentage by multiplying this result by 100%:

`P(7\&E)=0.125\cdot100\%=12.5\%`

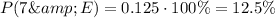
Answer: 12.5%