Given:
Two dice are rolled.
Required:
Probability of getting a sum of 5 or 9 on a roll of two dice.
Are these two events overlapping or non overlapping.
Step-by-step explanation:
The sample space of the event when two dice is rolled is given by

This is the sample space when two dice are rolled
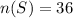
Event 1 : getting a sum of 5 when two dice are rolled
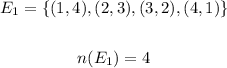
Probability of getting a sum of 5 when two dice are rolled is the ratio of number of outcomes in event E₁ to the number of outcomes in sample space.
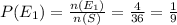
Now the second event is getting a sum of 9 when two dice are rolled
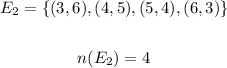
Probability of getting a sum of 9 when two dice are rolled is the ratio of number of outcomes in event E₂ to the number of outcomes in sample space.
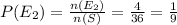
If we see both the events there are no sub events that are common in E₁ and E₂
So the events are non-overlapping.
The probability of combined event is given as the sum of probability of both the events

Final answer:
The individual events are non-overlapping.
The probability of the combined event is 2/9.