Question

Hi! I have the answers to A. AND B. which arek=1.24% for aand k= 0.20% for b

Answer 1

Explanation:

We have that the population function has the following form:

`y=A\cdot e^(kt)`

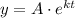
Where y is the population after t time, A is the initial population and k is the growth constant.

Therefore, for each case, we calculate the value of k:

(a)

t = 4

y = 1375000

A = 1309000

Solving for k:

`\begin{gathered} 1375000=1309000\cdot\: e^(k\cdot4) \\ e^(4k)=(1375000)/(1309000) \\ 4k=\ln \: \mleft((1375000)/(1309000)\mright) \\ k=(\ln\mleft((1375000)/(1309000)\mright))/(4) \\ k=0.01229\cong0.0123\rightarrow1.23\text{\%} \end{gathered}`

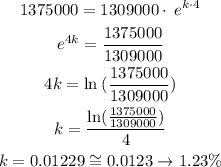
(b)

t = 4

y = 1386000

A = 1375000

Solving for k:

`\begin{gathered} 1386000=1375000\cdot\: e^(k\cdot4) \\ e^(4k)=(1386000)/(1375000) \\ 4k=\ln \: \: \: \mleft((1386000)/(1375000)\mright) \\ k=(\ln \mleft((1386000)/(1375000)\mright))/(4) \\ k=0.00199\cong0.002\rightarrow0.20\text{\%} \end{gathered}`

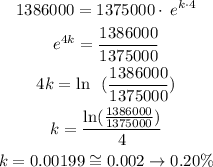
(c)

To compare we calculate the quotient between both periods: