Given that the resistances are connected in parallel.
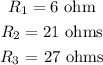
Also, the total voltage is 7 V.
The formula to find the equivalent resistance connected in parallel is
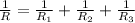
Substituting the values, the resistance will be
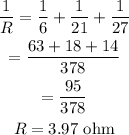
Thus, the total resistance of the circuit is 3.97 ohms.