Question

About % of tomato plants have agreater than or equal 3.22 feet. Round thtwo decimal places, if necessary.The heights of tomato plants are Normally distributedwith a mean of 3.56 feet and a standard deviation of 0.25foot.About what percent of tomato plants have a heightgreater than or equal to 3.22 feet?Use the z-table to answer the question.

Answer 1

91.31 %

Explanation:

edge 2023

Answer 2

`\begin{gathered} \text{Given} \\ \mu=3.56 \\ \sigma=0.25 \\ x=3.22 \end{gathered}`

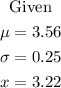
First, find the z-value of the given sample

`\begin{gathered} z=(x-\mu)/(\sigma) \\ z=(3.22-3.56)/(0.25) \\ z=(-0.34)/(0.25) \\ z=-1.36 \end{gathered}`

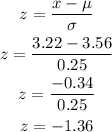
Now that we have the z-score, find P(Z > -1.36)

The area to the left of z-score, when z = -1.36 is equal to 0.08691.

Use this to solve for P(Z > -1.36)

`\begin{gathered} P(z>-1.36)=1-0.08691 \\ P(z>-1.36)=0.91309 \end{gathered}`

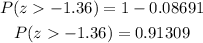
Multiply by 100% to get the percentage and we have

`0.91309\cdot100\%=91.309\%`

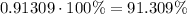
Rounding the answer to two decimal places, the percentage of tomato plants that has a height of 3.22 feet or greater is 91.31%.