Question

The topic is solving radical equations, but im just confused on whether to squafe it or not
`2 √(n) = n - 3`

Answer 1

a We are given the following radical equation

`2\sqrt[]{n}=n-3`

To solve this equation we need to square both sides of the equation

`\begin{gathered} (2\sqrt[]{n})^2=(n-3)^2 \\ 4n=(n-3)^2 \end{gathered}`

Apply the squares formula on right-hand side of the equation

`(a-b)^2=a^2+b^2-2ab`

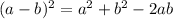
So the equation will become

`\begin{gathered} 4n=n^2+3^2-2(n)(3) \\ 4n=n^2+9-6n \\ 0=n^2+9-6n-4n \\ 0=n^2+9-10n \\ n^2-10n+9=0 \end{gathered}`

So we are left with a quadratic equation.

The standard form of a quadratic equation is given by

`ax^2+bx+c=0`

Comparing the standard equation with our equation we get the following coefficients

a = 1

b = -10

c = 9

Now recall that quadratic formula is given by